1.3. Mehrschrittverfahren für Anfangswertprobleme

Im vorangegangenen Abschnitt haben wir Einschrittverfahren betrachtet, die zur Berechnung einer numerischen Approximation der unbekannten Lösung \(u_\tau(t_{k+1}) \in \R^n\) lediglich Informationen aus dem letzten Zeitschritt \(t_k \in \Omega_\tau \subset [0, T]\) verwendet haben. Dies erinnert ein wenig an Markow-Prozesse aus der Stochastik, die nur auf Informationen des aktuellen Zustands zurückgreifen und ansonsten gedächtnislos sind. Da sich das Verhalten einer Lösungsfunktion \(u_\tau\) nur schwer mit Hilfe eines einzigen Datenpunkts vorhersagen lässt, ist es sinnvoll auch die Werte der vorangehenden Zeitschritte zu berücksichtigen. Dieser Ansatz führt zu den sogenannten Mehrschrittverfahren für Anfangswertprobleme.

Konkret verwenden wir nun zur Berechnung der numerischen Approximation \(u_\tau(t_{k+s})\) die bereits berechneten Werte der Zeitschritte \(t_k, \ldots, t_{k+s-1} \in \Omega_\tau\) für eine Zeitdiskretisierung \(\Omega_\tau\) des Intervalls \([0,T]\). Hierbei bezeichnen wir mit \(s \in \N^+\) die Stufe des Mehrschrittverfahrens. Die bereits in Einschrittverfahren für Anfangswertprobleme diskutierten Einschrittverfahren lassen sich dementsprechend als Mehrschrittverfahren der Stufe \(s=1\) interpretieren. Wir werden in diesem Abschnitt die abkürzende Notation \(F_k \coloneqq F(t_k,u_\tau(t_k))\) verwenden.

Wir betrachten zunächst einige einfache Beispiele für Mehrschrittverfahren der Stufe \(s=2\).

Beispiel 1.9 (Mehrschrittverfahren für Stufe s=2)

Die beiden folgenden Beispiele erklären Mehrschrittverfahren der Stufe \(s=2\), d.h., wir verwenden zur Berechnung der numerischen Approximation \(u_\tau(t_{k+2})\) die beiden vorigen Zeitschritte \(t_k, t_{k+1} \in \Omega_\tau\). Die Grundidee ist es passende Quadraturformeln (siehe [TR]) für die Approximation des Integrals auf der rechten Seite folgender Gleichung zu benutzen:

\[u_\tau(t_{k+2}) - u_\tau(t_{k}) \ = \ \int^{t_{k+2}}_{t_{k}} u'_\tau(t) \, \mathrm{d}t \ = \ \int^{t_{k+2}}_{t_{k}} F(t, u_\tau(t)) \, \mathrm{d}t.\]

1. Verwenden wir zunächst die simple Mittelpunktsregel zur Approximation des Integrals im Intervall \([t_{k}, t_{t+2}]\), so erhalten wir

   \[\begin{split}\begin{split} u_\tau(t_{k+2}) - u_\tau(t_{k}) \ &= \ \int^{t_{k+2}}_{t_{k}} F(t, u_\tau(t)) \, \mathrm{d}t \\ &\approx \ (t_{k+2} - t_{k}) \cdot F\left(\frac{t_{k} + t_{k+2}}{2}, u_\tau\left(\frac{t_{k} + t_{k+2}}{2}\right)\right)\\ &= \ 2\tau \cdot F(t_{k+1}, u_\tau(t_{k+1})). \end{split}\end{split}\]

   Durch Umstellen erhalten wir so ein explizites Verfahren zur Berechnung des nächsten Werts \(u_\tau(t_{k+2})\) der numerischen Approximation aus den letzten beiden Werten, nämlich

   \[u_\tau(t_{k+2}) \ = \ u_\tau(t_{k}) + 2\tau \cdot F_{k+1}.\]

2. Verwenden wir stattdessen die Simpsonregel als interpolatorische Quadraturformel für die Approximation des Integrals im Intervall \([t_{k}, t_{t+2}]\), so erhalten wir

   \[\begin{split}\begin{split} u_\tau(t_{k+2}) \! - \! u_\tau(t_{k}) \, &= \, \int_{t_{k}}^{t_{k+2}} F(t, u_\tau(t)) \, \mathrm{d}t \\ &\approx \, \frac{t_{k+2} - t_{k}}{6} \cdot \Bigl( F(t_{k}, u_\tau(t_{k})) \\ & \hspace{2.05cm} \left. + \ 4\cdot F\left(\frac{t_{k} + t_{k+2}}{2}, u_\tau\left(\frac{t_{k} + t_{k+2}}{2}\right) \right) \right. \\ & \hspace{2.05cm} + F(t_{k+2}, u_\tau(t_{k+2}))\Bigr)\\ &= \, \frac{\tau}{3} \cdot \left( F(t_{k},u_\tau(t_{k}))+ 4 F(t_{k+1},u_\tau(t_{k+1})) + F(t_{k+2},u_\tau(t_{k+2})) \right)\!. \end{split}\end{split}\]

   Durch Umstellen erhalten wir so ein implizites Verfahren zur Berechnung des nächsten Werts \(u_\tau(t_{k+2})\) der numerischen Approximation aus den letzten beiden Werten, nämlich

   \[\begin{split} u_{\tau}(t_{k+2}) \, = \, u_\tau(t_{k}) + \frac{\tau}3 \cdot ( F_{k} + 4 \cdot F_{k+1} + F_{k+2}). \end{split}\]

Die in Beispiel 1.9 illustrierten Mehrschrittverfahren sind beide von einer linearen Gestalt, die in folgender Definition verallgemeinert wird.

Definition 1.11 (Lineare Mehrschrittverfahren)

Sei eine Zeitdiskretisierung \(\Omega_\tau \coloneqq \lbrace t_k \in [0,T] \colon t_k \coloneqq k \cdot \tau, k = 0,\ldots, N \rbrace\) für ein gegebenes Intervall \([0,T] \subset \R_0^+\) mit Zeitschrittweite \(\tau \coloneqq \frac{T}{N}\) für \(N \in \N^+\) eines Anfangswertproblems der Form \(u'(t) = F(t,u(t))\) für \(t \in [0,T]\) mit \(u(0) \coloneqq u_0 \in \R^n\) gegeben.

Wir nennen ein Mehrschrittverfahren der Stufe \(s \in \N^+\) linear, wenn es sich in folgender Form schreiben lässt:

(1.14)\[\begin{split}\begin{split} \sum_{i=0}^s \alpha_i u_\tau(t_{k+i}) \ &= \ \alpha_0 u_\tau(t_{k}) + \alpha_{1} u_\tau(t_{k+1})+\ldots+\alpha_s u_\tau(t_{k+s})\\ &= \ \tau \cdot (\beta_0 F_{k} + \beta_{1} F_{k+1}+\ldots+\beta_s F_{k+s} ) \ = \ \tau \cdot \sum_{i=0}^s \beta_i F_{k+i}, \end{split}\end{split}\]

mit Koeffizienten \(\alpha_i, \beta_i \in \R\) für \(i=0,\ldots,s\).

Wir nennen das lineare Mehrschrittverfahren explizit falls \(\beta_s = 0\) gilt und ansonsten implizit.

Lineare Mehrschrittverfahren sind mit Abstand die gebräuchlichsten Methoden in der Numerik und daher werden wir uns im Folgenden auf diese Klasse von Verfahren einschränken. Damit wir wirklich ein \(s\)-stufiges lineares Mehrschrittverfahren vorliegen haben, werden wir immer annehmen, dass \(\alpha_s \neq 0\) und \(|\alpha_0|+|\beta_0|> 0\) in Definition 1.11 gilt. An der Form eines linearen Mehrschrittverfahrens in (1.14) sehen wir ebenfalls einen allgemeinen Vorteil gegenüber den Einschrittverfahren in Einschrittverfahren für Anfangswertprobleme: Wir können in jeder Iteration \(k=0,\ldots,N-s\) zur Bestimmung des Werts \(u_\tau(t_{k+s}) \in \R^n\) auf bereits angenäherte Funktionsauswertungen \(F_k, \ldots, F_{k+s-1} \in \R^n\) zurückgreifen und müssen nur eine einzige neue Funktionsauswertung \(F_{k+s} \in \R^n\) berechnen.

Bei der numerischen Berechnung gehen wir analog wie bei Einschrittverfahren vor. Wir müssen nur zusätzlich zu \(u_\tau(t_{k+s-1}) \in \R^n\) auch die Werte \(u_\tau(t_{k}),\ldots,u_\tau(t_{k+s-2}) \in \R^n\) verwenden. Hierdurch ensteht ein effektiver Unterschied zu Einschrittverfahren mit Bezug auf die benötigten Anfangswerte. Um ein Mehrschrittverfahren der Stufe \(s>1\) durchzuführen benötigen wir nicht nur den gegebenen Anfangswert \(u_0 \in \R^n\), sondern auch numerische Approximationen der folgenden \(s-1\) Werte \(u_\tau(t_1),\ldots,u_\tau(t_{s-1})\) zur Berechnung des Wertes \(u_\tau(t_{s})\). Da diese numerischen Approximationen zunächst unbekannt sind müssen wir sie erst durch ein anderes Verfahren, etwa ein Einschrittverfahren, berechnen. Dabei müssen wir insbesondere darauf achten, dass das gewählte Verfahren von der selben Konvergenzordnung wie das Mehrschrittverfahren gewählt wird, um diese insgesamt nicht zu verkleinern. Eine Diskussion der Konsistenz- und Konvergenzordnung von Mehrschrittverfahren folgt in Konsistenz von Mehrschrittverfahren.

Bemerkung 1.2 (Wohldefiniertheit von Mehrschrittverfahren)

Bei expliziten Verfahren, d.h. \(\beta_s = 0\), ist die Wohldefiniertheit des Mehrschrittverfahrens natürlich gegeben, da eine numerische Approximation \(u_\tau(t_{k+1}) \in \R^n\) explizit bestimmt werden kann. Im impliziten Fall, d.h. für \(\beta_s \neq 0\), ist die Existenz einer Lösung des auftretenden nichtlinearen Gleichungssystems jedoch im Allgemeinen nicht gesichert. Hier benötigen wir wieder das in Existenz und Eindeutigkeit von Lösungen diskutierte Fixpunktargument um die Wohldefiniertheit der beschriebenen Verfahren zu gewährleisten.

Es lässt sich zeigen, dass folgende Aussage gilt: Für eine stetige Funktion \(F\) des Anfangswertproblems \(u'(t) = F(t, u(t)), u(0) = u_0 \in \R^n\), die bezüglich des zweiten Arguments Lipschitz-stetig mit Lipschitz-Konstante \(L > 0\) ist, existiert eine eindeutige Lösung \(u_\tau(t_{k+s}) \in \R^n\) des Mehrschrittverfahrens (1.14) falls für die Schrittweite \(\tau < \frac{|\beta_s|}{|\alpha_s|} \cdot L\) gilt.

1.3.1. Konsistenz von Mehrschrittverfahren

Während wir die Konvergenzordnung analog zu Einschrittverfahren definieren können, benötigen wir noch eine passende Definition von Konsistenz für Mehrschrittverfahren. Wir führen dazu zunächst den lokalen Konsistenzfehler eines Mehrschrittverfahrens ein

(1.15)\[\begin{split}\begin{split} g_\tau(t_k) \ &\coloneqq \ \frac{1}\tau \sum_{i=0}^s \alpha_i u(t_{k+i}) - \sum_{i=0}^s \beta_i F(t_{k+i},u(t_{k+i})) \\ &= \ \frac{1}\tau \sum_{i=0}^s \alpha_i u(t_{k+i}) - \sum_{i=0}^s \beta_i u'(t_{k+i}) \qquad k=0,\ldots,N-s. \end{split}\end{split}\]

Hierbei haben wir analog zum Fall von Einschrittverfahren wieder die echte Lösung \(u \colon [0,T] \rightarrow \R^n\) in das Mehrschrittverfahren eingesetzt. Basierend auf dem lokalen Konsistenzfehler (1.15) können wir nun definieren wann ein Mehrschrittverfahren konsistent ist.

Definition 1.12 (Konsistenz von linearen Mehrschrittverfahren)

Ein lineares Mehrschrittverfahren heißt konsistent, falls der globale Konsistenzfehler

\[K_\tau \coloneqq \max_{k=0,\ldots,N-s} || g_\tau(t_k) ||\]

gegen Null konvergiert für \(\tau \rightarrow 0\).

Das Verfahren heißt konsistent von der Ordnung \(p\), falls \(K_\tau = {\cal O}(\tau^p)\) für \(\tau \rightarrow 0\).

Wir können zunächst ein schönes Resultat zur Charakterisierung der Konsistenz eines linearen Mehrschrittverfahren herleiten.

Lemma 1.6 (Konsistenzbedingung für Mehrschrittverfahren)

Ein lineares Mehrschrittverfahren der Stufe \(s \in \N^+\) ist konsistent von der Ordnung \(p\in \N^+\), wenn die folgenden Gleichungen gelten

\[\sum_{i=0}^s \alpha_i i^m \ = \ m \cdot \sum_{i=0}^s \beta_i i^{m-1} , \qquad m=0,1,\ldots,p.\]

Hierbei verwenden wir die Konvention \(0^0 \coloneqq 1\).

Proof. Es sei \(s \in \N^+\) die Stufe des Mehrschrittverfahrens und \(u \colon [0, T] \rightarrow \R^n\) die echte Lösung des Anfangswertproblems (1.1) für die wir annehmen, dass \(u \in C^p([0,T])\) gilt. Um zu zeigen, dass das Verfahren konsistent von der Ordnung \(p \in \N^+\) ist, müssen wir gemäß Definition 1.12 zeigen, dass für den global Konsistenzfehler gilt:

\[K_\tau \ \coloneqq \ \max_{k=0,\ldots,N-s} \left\Vert \frac{1}\tau \sum_{i=0}^s \alpha_i u(t_{k+i}) - \sum_{i=0}^s \beta_i u'(t_{k+i}) \right\Vert \in \mathcal{O}(\tau^p).\]

Sei im weiteren \(k \in \lbrace 0,\ldots,N-s\rbrace\) der Index des Zeitschritts für den die Norm des lokalen Konsistenzfehlers \(g_\tau(t_k)\) maximal wird. Wir betrachten zunächst die Taylorentwicklung des linken Terms im Zeitschritt \(t_k \in \Omega_\tau\) wie folgt:

\[\begin{split}\begin{split} \frac{1}{\tau} \sum_{i=0}^s \alpha_i u(t_{k+i}) \ = \ \frac{1}{\tau} \Bigl( \alpha_0 u(t_k) &+ \alpha_1 (u(t_k) + \tau u'(t_k) + \frac{\tau^2}{2} u''(t_k) + \, \ldots) \\ &+ \alpha_2 (u(t_k) + 2\tau u'(t_k) + \frac{(2\tau)^2}{2} u''(t_k) + \, \ldots) \\ &\vdots\\ &+ \alpha_s (u(t_k) + s\tau u'(t_k) + \frac{(s\tau)^2}{2} u''(t_k) + \, \ldots) \Bigr) \end{split}\end{split}\]

Dies können wir zusammenfassen zu

\[\begin{split}\begin{split} \frac{1}{\tau} \sum_{i=0}^s \alpha_i u(t_{k+i}) \ &= \ \frac{1}{\tau} \sum_{m=0}^p \sum_{i=0}^s \alpha_i \frac{i^m \tau^m}{m!} u^{(m)}(t_{k}) + \mathcal{O}(\tau^{p}) \\ &= \ \sum_{m=0}^p \sum_{i=0}^s \alpha_i i^m \frac{\tau^{m-1}}{m!} u^{(m)}(t_{k}) + \mathcal{O}(\tau^{p}) \end{split}\end{split}\]

Betrachten wir nun die Taylorentwicklung des rechten Terms im Zeitschritt \(t_k \in \Omega_\tau\):

\[\begin{split}\begin{split} \sum_{i=0}^s \beta_i u'(t_{k+i}) \ = \ \beta_0 u'(t_k) &+ \beta_1 (u'(t_k) + \tau u''(t_k) + \frac{\tau^2}{2} u'''(t_k) + \, \ldots )\\ &+ \beta_2 (u'(t_k) + 2\tau u''(t_k) + \frac{(2\tau)^2}{2} u'''(t_k) + \, \ldots )\\ &\vdots\\ &+ \beta_s (u'(t_k) + s\tau u''(t_k) + \frac{(s\tau)^2}{2} u'''(t_k) + \, \ldots )\\ \end{split}\end{split}\]

Dies können wir wiederum zusammenfassen zu

\[\begin{split}\begin{split} \sum_{i=0}^s \beta_i u'(t_{k+i}) \ &= \ \sum_{m=0}^p \sum_{i=0}^s \beta_i \frac{i^m \tau^m}{m!} u^{(m+1)}(t_{k}) + \mathcal{O}(\tau^{p}) \\ &= \ \underbrace{0\cdot \sum_{i=0}^s \beta_i i^{-1} \frac{\tau^0}{(0+1)!} u^{0}(t_{k})}_{=\:0} \\ &\hspace{2cm} + \sum_{m=0}^p (m+1) \cdot \sum_{i=0}^s \beta_i i^m \frac{\tau^m}{(m+1)!} u^{(m+1)}(t_{k}) + \mathcal{O}(\tau^{p})\\ &= \ 0\cdot \sum_{i=0}^s \beta_i i^{-1} \frac{\tau^0}{(0+1)!} u^{0}(t_{k}) \\ &\hspace{2cm} + \sum_{m=1}^p m \cdot \sum_{i=0}^s \beta_i i^{m-1} \frac{\tau^{m-1}}{m!} u^{(m)}(t_{k}) + \mathcal{O}(\tau^{p})\\ &= \ \sum_{m=0}^p m \cdot \sum_{i=0}^s \beta_i i^{m-1} \frac{\tau^{m-1}}{m!} u^{(m)}(t_{k}) + \mathcal{O}(\tau^{p}) \end{split}\end{split}\]

Insgesamt gilt also für den globalen Konsistenzfehler

\[K_\tau \ = \ \left\Vert \sum_{m=0}^p \sum_{i=0}^s \alpha_i i^m \frac{\tau^{m-1}}{m!} u^{(m)}(t_{k}) - \sum_{m=0}^p m \cdot \sum_{i=0}^s \beta_i i^{m-1} \frac{\tau^{m-1}}{m!} u^{(m)}(t_{k}) + \mathcal{O}(\tau^{p}) \right\Vert\]

Ein Koeffizientenvergleich der beiden Terme zeigt uns, dass \(K_\tau \in \mathcal{O}(\tau^p)\) gilt wenn folgende Bedingungen erfüllt sind:

\[\sum_{i=0}^s \alpha_i i^m \ = \ m \cdot \sum_{i=0}^s \beta_i i^{m-1}, \qquad m=0,\ldots,p.\]

◻

Um eine möglichst hohe Konsistenzordnung für ein \(s\)-stufiges Mehrschrittverfahren zu erhalten müssen wir wir analog zu den Einschrittverfahren in Einschrittverfahren für Anfangswertprobleme Gleichungssysteme für die Koeffizienten lösen, wie wir im folgenden Beispiel sehen werden.

Beispiel 1.10 (Konsistenzordnung von Mehrschrittverfahren)

In diesem Beispiel wollen wir Mehrschrittverfahren der Stufen \(s = 1\) und \(s=2\) bezüglich ihrer Konsistenzordnung \(p \in \N^+\) untersuchen. Hierzu verwenden wir die Konsistenzbedingung aus Lemma 1.6 mit

\[\sum_{i=0}^s \alpha_i i^m \ = \ m \cdot \sum_{i=0}^s \beta_i i^{m-1}, \qquad m=0,\ldots,p.\]

1. Im Fall eines Mehrschrittverfahrens der Stufe \(\mathbf{s=1}\) gilt für die erste Bedingung mit \(m=0\) und der Konvention \(0^0 \coloneqq 1\):

   \[\alpha_0 \cdot 0^0 + \alpha_1 \cdot 1^0 \ = \ \alpha_0 + \alpha_1 \ \overset{!}{=} \ 0.\]

   Hieraus lässt sich also ableiten, dass \(\alpha_0 = - \alpha_1\) gelten muss. Ohne Beschränkung der Allgemeinheit können wir \(\alpha_1=1\) und \(\alpha_0=-1\) normieren. Betrachten wir nun die zweite Bedingung für \(m=1\), so erhalten wir:

   \[\alpha_0 \cdot 0^1 + \alpha_1 \cdot 1^1\ = \ \alpha_1 \ \overset{!}{=} \ 1 \cdot ( \beta_0 \cdot 0^0 + \beta_1 \cdot 1^0 ) \ = \ \beta_0 + \beta_1.\]

   Durch die Normierung von \(\alpha_1 = 1\) sehen wir also, dass \(\beta_0 + \beta_1 = 1\) gelten muss, um Konsistenzordnung \(p=s=1\) zu erreichen. Diese Bedingungen werden unter anderem durch das Vorwärts-Euler Verfahren (\(\beta_0=1, \beta_1=0\)), das Rückwärts-Euler Verfahren (\(\beta_0=0, \beta_1=1\)) und das Crank-Nicholson Verfahren (\(\beta_0 = \beta_1=\frac{1}2\)) aus Einschrittverfahren für Anfangswertprobleme erfüllt.

2. Im Fall eines Mehrschrittverfahrens der Stufe \(\mathbf{s=2}\) gilt für die erste Bedingung mit \(m=0\) und der Konvention \(0^0 \coloneqq 1\):

   \[\alpha_0 \cdot 0^0 + \alpha_1 \cdot 1^0 + \alpha \cdot 2^0 \ = \ \alpha_0 + \alpha_1 + \alpha_2 \ \overset{!}{=} \ 0.\]

   Für die zweite Bedingung mit \(m=1\) erhalten wir

   \[\alpha_0 \cdot 0^1 + \alpha_1 \cdot 1^1 + \alpha_2 \cdot 2^1 \ = \ \alpha_1 + 2 \alpha_2 \ \overset{!}{=} \ 1 \cdot (\beta_0 \cdot 0^0 + \beta_1 \cdot 1^0 + \beta_2 \cdot 2^0) \ = \ \beta_0 + \beta_1 + \beta_2.\]

   Und für die dritte Bedingung mit \(m=2\) erhalten wir

   \[\alpha_0 \cdot 0^2 + \alpha_1 \cdot 1^2 + \alpha \cdot 2^2\ = \ \alpha_1 + 4 \alpha_2 \ \overset{!}{=} \ 2 \cdot (\beta_0 \cdot 0^1 + \beta_1 \cdot 1^1 + \beta_2 \cdot 2^1) \ = \ 2\beta_1 + 4\beta_2.\]

   Insgesamt müssen wir also für ein Mehrschrittverfahren der Stufe \(s=2\) und Konsistenzordnung \(p=2\) folgendes unterbestimmte Gleichungssystem lösen:

   \[\alpha_0+\alpha_1+\alpha_2 \: = \: 0, \qquad \alpha_1+2 \alpha_2 \: = \: \beta_0+\beta_1+\beta_2 , \qquad \alpha_1+4\alpha_2 \: = \: 2\beta_1+4\beta_2.\]

   Wir sehen, dass die Mittelpunktsregel mit \(\alpha_0=-1,\alpha_1=0,\alpha_2=1\) sowie \(\beta_0 =\beta_2=0, \beta_1=2\) eine mögliche Lösung dieses Systems liefert.

1.3.2. Stabilität von Mehrschrittverfahren

Nachdem wir die Konsistenzordnung von Mehrschrittverfahren untersucht haben stellt sich die Frage, ob wir die gleiche Konvergenzordnung erreichen können. Im Fall von Einschrittverfahren hatten wir festgestellt, dass für Lipschitz-stetige Funktionen \(F\) auf der rechten Seite des Anfangswertproblems (1.1) aus Konsistenz bereits Konvergenz folgt. Leider ist die Situation für Mehrschrittverfahren deutlich komplizierter, wie das folgende Beispiel zeigt.

Beispiel 1.11 (Instabilität eines Mehrschrittverfahrens)

Es werde ein Verfahren möglichst hoher Ordnung der Form

\[u_\tau(t_{k+2}) - (1 + \alpha) u_\tau(t_{k+1}) + \alpha u_\tau(t_k) \ = \ \tau \cdot \left( \frac{3-\alpha}{2}F_{k+1} - \frac{1+\alpha}{2}F_k \right)\]

gesucht für eine Funktion \(F \in C^3([0,T] \times \R^n; \R^n)\).

Wir bestimmen den Koeffizienten \(\alpha \in \R\) mittels Taylorentwicklung so, dass eine möglichst hohe Konsistenzordnung erreicht wird indem wir wieder den lokalen Konsistenzfehler in \(t_k \in \Omega_\tau\) betrachten:

\[\begin{split}\begin{split} g_\tau(t_k) \ &= \ \frac{1}{\tau} \cdot \left( u(t_{k+2}) - (1 + \alpha) u(t_{k+1}) + \alpha u(t_k) \right) - \frac{3-a}{2}u'(t_{k+1}) + \frac{1+\alpha}{2}u'(t_k)\\ &= \ u'(t_k) \cdot \underbrace{\left( 2 - (1+\alpha) + \alpha - \frac{3-\alpha}{2} + \frac{1+\alpha}{2}\right)}_{= \: 0}\\ &+ \ u''(t_k) \cdot \underbrace{\left( \frac{4\tau}{2} -(1+\alpha) \frac{\tau}{2} - \frac{3-\alpha}{2}\tau\right)}_{= \: 0}\\ &+ \ u'''(t_k) \cdot \underbrace{\left( \frac{8}{6}\tau^2 -(1+\alpha) \frac{\tau^2}{6} - \frac{3-\alpha}{2}\cdot\frac{\tau^2}{2}\right)}_{= \: \frac{\tau^2}{12}(5+\alpha)} \ + \ \mathcal{O}(\tau^3). \end{split}\end{split}\]

Also erhalten wir eine Konsistenzordnung von \(p=3\) für \(\alpha = -5\) und \(p=2\) in allen anderen Fällen. Wir erwarten eine entsprechende Konvergenzordnung für das Verfahren. Ein numerisches Experiment zeigt uns jedoch ein völlig anderes Ergebnis.

Wie man an den beiden Illustrationen in Abb. 1.1 erkennen kann ist das Verhalten des numerischen Algorithmus für unterschiedliche Wahlen von \(\alpha \in \R\) vollkommen unterschiedlich. Bei näherer Betrachtung stellt sich heraus, dass das Mehrschrittverfahren für \(\alpha > 1\) und \(\alpha < -1.5\) divergiert trotz einer Konsistenzordnung von mindestens Zwei. Dies liegt daran, dass das lineare Mehrschrittverfahren in diesen Fällen nicht stabil ist.

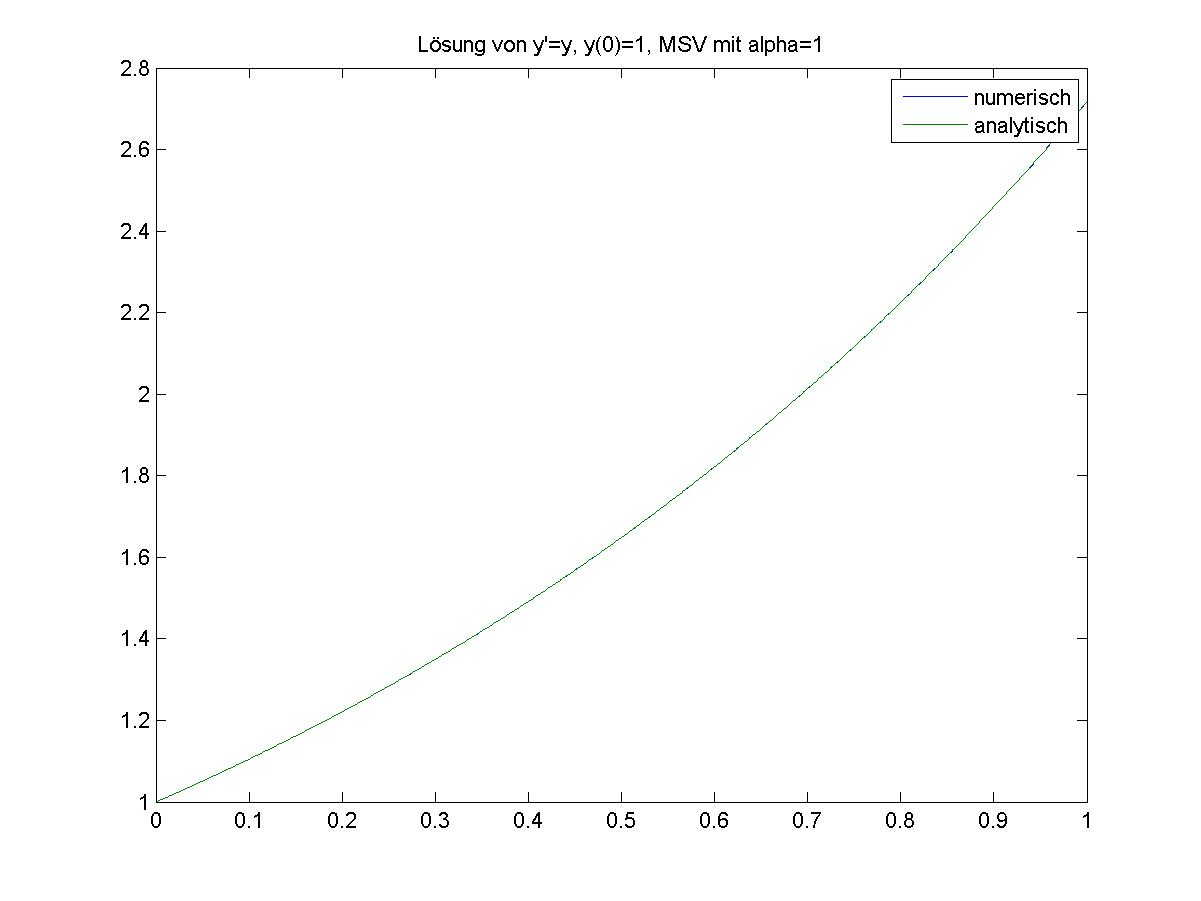
Abb. 1.1 Visualisierung der numerischen Approximation einer Lösung eines Anfangswertproblems mit dem linearen Mehrschrittverfahren aus Beispiel 1.11 für die Wahl des Parameters \(\alpha=1\) (oben) und \(\alpha = -1.5\) (unten). Entnommen aus [Wubb]

Motiviert durch das obige Beispiel wollen wir uns also im Folgenden mit der Stabilitätsanalyse von Mehrschrittverfahren beschäftigten. Wir folgen dabei grob der Struktur in [Wuba].

Die grundlegende Idee ist es nun die Stabilität eines linearen Mehrschrittverfahrens für eine möglichst einfache Differentialgleichung zu untersuchen. Wenn ein konsistentes Verfahren konvergent ist, dann muss es insbesondere konvergent sein für die einfachste aller Anfangswertaufgaben. Daher betrachten wir das sogenannte Modellproblem

(1.16)\[u'(t) \, = \, 0, \qquad u(0) \, = \, 0,\]

mit der Lösung \(u(t) \equiv 0\). Die durch das numerische Verfahren gelieferte Lösung muss also für \(\tau \rightarrow 0\) gleichmäßig gegen die Nullfunktion konvergieren. Das folgende Lemma besagt, dass diese Bedingung schon ausreicht, damit das numerische Verfahren für alle Anfangswertaufgaben konvergent ist.

Lemma 1.7 (Reduktion auf das Modellproblem)

Gegeben sei ein lineares Mehrschrittverfahren der Stufe \(s\in \N^+\). Sei \((\Omega_{\tau_k})_{k\in\N}\) eine Folge von äquidistanten Zeitdiskretisierungen mit Zeitschrittweiten \(\tau_k > 0, k\in\N\). Falls für jede Wahl der Startwerte \(u_\tau(t_i) \in \R^n\) mit

\[u_{\tau_k}(t_i) \ \overset{\tau_k \rightarrow 0}{\longrightarrow} \ 0, \qquad i = 0,\ldots,s-1\]

die Folge \((u_{\tau_k})_{k\in\N}\) der numerischen Approximationen für das Modellproblem gegen die Nullfunktion konvergiert, so ist das Mehrschrittverfahren stabil für alle Anfangswertaufgaben.

Proof. Siehe [Wubb]. ◻

Wenn wir also nun ein lineares Mehrschrittverfahren für das Modellproblem (1.16) betrachten, so stellen wir fest, dass für die rechte Seite der gewöhnlichen Differentialgleichung \(F(t, u(t)) \equiv 0\) gilt und somit für das Mehrschrittverfahren \(\sum_{i=0}^s \beta_i F_{k+i} = 0\) ist für alle \(k=0,\ldots,N-s\). Somit reduziert sich das lineare Mehrschrittverfahren mit gegebenen Koeffizienten \(\alpha_i \in \R, i=0,\ldots,s\) auf die Lösung des folgenden Gleichungssystems:

(1.17)\[\sum_{i=0}^s \alpha_i u_\tau(t_{k+i}) \ = \ 0, \qquad k = 0,\ldots, N-s.\]

Ein Problem dieser Form ist bekannt als lineare, homogene Differenzengleichung mit konstanten Koeffizienten \(\alpha_i \in \R, i=0,\ldots,s\).

Aus diesem Grund werden wir uns im Folgenden auf einige mathematische Resultate aus der Theorie der linearen Differenzengleichungen stützen, die wir in dieser Vorlesung jedoch nur im Ansatz diskutieren können. Wir wollen deswegen mit einer grundlegenden Definition beginnen.

Definition 1.13 (Lineare Differenzengleichung)

Eine lineare Differenzengleichung \(s\)-ter Ordnung über einem Körper \(\mathbb{K}\) ist von der Form

(1.18)\[\sum_{i=0}^s \alpha_i(k) f_{k+i} \ = \ \beta_k, \qquad k\in\N,\]

wobei die Koeffizienten \(\alpha_i \colon \N \rightarrow \mathbb{K}, i=0,\ldots,s\) Folgen sind, für die \(\alpha_s(k) \neq 0\) gilt für alle \(k \in \N\). Ist \((\beta_k)_{k\in\N} \subset \mathbb{K}\) die konstante Nullfolge, so nennen wir die Differenzengleichung homogen und ansonsten inhomogen.

Eine unendliche Zahlenfolge \(F = f_0, f_1, f_2, \ldots\), die für alle \(k\in\N\) die lineare Differenzengleichung (1.18) erfüllt, heißt Lösung der Differenzengleichung.

Die folgende Bemerkung erlaubt es uns eine lineare Differenzenfolge in eine explizite Form zu überführen, so dass Folgeglieder der Lösung aus gegebenen Anfangswert berechnet werden können.

Bemerkung 1.3 (Explizite Form von Differenzengleichungen)

Es ist klar, dass man eine lineare Differenzengleichung mit einem beliebigen Faktor aus \(\mathbb{K}\) multiplizieren kann ohne dessen Lösung zu verändern. Wenn man also die Koeffizientenfolgen \((\alpha_i(k))_{k\in\N}\) normiert, so dass \(\alpha_s(k) = -1\) für alle \(k \in \N\) gilt, so lässt sich eine Rechenvorschrift für das Folgenglied \(f_{k+s}\) explizit angeben als

\[f_{k+s} \ = \ \sum_{i=0}^{s-1} \alpha_i(k) f_{k+i} - \beta_k.\]

Für gegebene Startwerte \(f_0, \ldots, f_{s-1} \in \mathbb{K}^n\) und Koeffizientenfolgen \((\alpha_i)_{k\in\N}, (\beta_k)_{k\in\N}\) lässt sich so eine Lösung \(F\) der Differenzengleichung bestimmen.

Die explizite Form einer linearen Differenzengleichung wird zur Konstruktion von bestimmten Folgen in der Mathematik genutzt, wie unter anderem im folgenden Beispiel erklärt ist.

Beispiel 1.12 (Fibonnaci Zahlen)

Ein berühmtes Beispiel einer linearen Differenzengleichung 2. Ordnung wird durch die Fibonacci-Folge gelöst, deren Folgenglieder sich berechnen lassen durch die Differenzengleichung

(1.19)\[f_{k+2} \ = \ f_{k} + f_{k+1} \qquad \Leftrightarrow \qquad f_{k+2} - f_{k+1} - f_{k} \ = \ 0.\]

Für die typischerweise gewählten Startwerte \(f_0 = f_1 \coloneqq 1\) ergibt sich hieraus die bekannte Fibonacci-Folge als Lösung der linearen Differenzengleichung mit:

\[F \ = \ 1, 1, 2, 3, 5, 8, 13, 21, 34, \ldots\]

Wir erkennen, dass die Differenzengleichung (1.19) homogen ist und konstante Koeffizientenfolgen \(\alpha_0 = \alpha_1 \equiv -1\) und \(\alpha_2 \equiv 1\) besitzt.

Wenn wir zeigen können, dass Lösungen der linearen Differenzengleichung (1.17) für alle Startwerte \(f_0,\ldots,f_{s-1} \in \mathbb{K}^n\) beschränkt sind, so lässt sich zeigen, dass der globale Konsistenzfehler \(K_\tau\) für das Modellproblem (1.16) gegen Null konvergiert und das lineare Mehrschrittverfahren nach Lemma 1.7 stabil ist für alle Anfangswertaufgaben. Um die Beschränktheit von Lösungen der linearen Differenzengleichung (1.17) zu untersuchen führen wir zunächst ein weiteres Hilfsmittel ein.

Definition 1.14 (Charakteristisches Polynom)

Für eine homogene, lineare Differenzengleichung der Ordnung \(s \in \N^+\) mit konstanten Koeffizienten \(\alpha_i \in \mathbb{K}, i=0,\ldots,s\) der Form (1.17) definieren wir das zugehörige charakteristische Polynom der Differenzengleichung \(\rho \colon \mathbb{K} \rightarrow \mathbb{K}\) als:

\[\rho(x) \ \coloneqq \ \sum_{i=0}^s \alpha_i x^i.\]

Das charakteristische Polynom einer Differenzengleichung sagt viel über das Verhalten von zugehörigen Lösungen aus und dient unter Anderem dazu ihre Beschränktheit zu zeigen, wie folgendes bekanntes Theorem aussagt.

Satz 1.4 (Wurzelbedingung von Dahlquist)

Alle Lösungen einer homogenen linearen Differenzengleichung mit charakteristi- schem Polynom \(\rho\) sind beschränkt genau dann, wenn für die Nullstellen \(\lambda_i \in \mathbb{K}, i=0,\ldots,s-1\) von \(\rho\) folgende zwei Bedingungen erfüllt sind:

1. \(|\lambda_i| \, \leq \, 1\),

2. \(|\lambda_i| \, = \, 1 \qquad \Rightarrow \qquad \sigma_i \, = \, 1\),

wobei \(\sigma_i \in \N^+\) die Vielfachheit der Nullstelle \(\lambda_i \in \mathbb{K}\) ist.

Proof. Siehe [Wubb]. ◻

Mit Hilfe der Wurzelbedingung von Dahlquist haben wir nun ein überprüfbares Kriterium um die Stabilität von linearen Mehrschrittverfahren zu überprüfen.

Korollar 1.2 (Konvergenz von linearen Mehrschrittverfahren)

Falls ein lineares Mehrschrittverfahren konsistent ist von der Ordnung \(p \in \N^+\) und die zugehörige lineare Differenzengleichung die Wurzelbedingung von Dahlquist in Satz 1.4 erfüllt, so ist das Mehrschrittverfahren konvergent von der Ordnung \(p\in \N^+\).

Es bleibt immer noch die Frage offen welche Konvergenzordnung wir wirklich erreichen können, d.h. welche Konsistenzordnung ein stabiles Verfahren maximal erreichen kann. Es gibt hierbei tatsächlich eine Einschränkung, wie folgende Bemerkung festhält.

Bemerkung 1.4

Ein lineares Mehrschrittverfahren der Stufe \(s\in \N^+\) sei konsistent von der Ordnung \(p \in \N^+\) und stabil. Dann gelten die folgenden Beschränkungen an die Konsistenzordnung des Verfahrens:

1. \(p\leq s+2\), wenn \(s\) gerade ist,

2. \(p \leq s+1\), wenn \(s\) ungerade.

Ist \(\frac{\beta_s}{\alpha_s} \leq 0\) (also insbesondere bei expliziten Verfahren) dann gilt sogar nur \(p\leq s\).

Wir wollen abschließend das Wurzelkriterium von Dahlquist anwenden, um die Stabiliät einiger Mehrschrittverfahren im Folgenden zu untersuchen.

Beispiel 1.13 (Stabilität von linearen Mehrschrittverfahren)

Wir werden im Folgenden die Stabilität von linearen Mehrschrittverfahren durch Betrachtung der Nullstellen der assoziierten charakteristischen Polynome analysieren.

1. Wir können Einschrittverfahren als Mehrschrittverfahren mit \(s = 1\) interpretieren. Sie sind von der Form

   \[u_\tau(t_{k+1}) - u_\tau(t_k) \ = \ f_\tau(t_k, u_\tau(t_k)),\]

   und damit ist das charakteristische Polynom der zugehörigen homogenen, linearen Differenzengleichung gegeben durch

   \[\rho(x) \ = \ x - 1.\]

   Die einzige (einfache) Nullstelle von \(\rho\) ist offensichtlich \(\lambda_0 = 1\). Also sind Einschrittverfahren stabil, was zu unseren Beobachtungen aus Einschrittverfahren für Anfangswertprobleme passt.

2. Wir betrachten als Nächstes ein lineares Mehrschrittverfahren das gegeben ist durch:

   \[u_\tau(t_{k+2}) - 2 u_\tau(t_{k+1}) + u_\tau(t_{k}) \ = \ 0.\]

   Unabhängig von der rechten Seite \(F(t,u(t))\) der Anfangswertaufgabe, die es zu lösen gilt, sehen wir ein, dass das Mehrschrittverfahren konsistent ist nach Beispiel 1.10 oben. Betrachten wir also das charakteristische Polynom der zugehörigen Differenzengleichung, das gegeben ist durch

   \[\rho(x) \ = \ x^2 -2x + 1.\]

   Dieses Polynom besitzt eine doppelte Nullstelle \(\lambda_0 = \lambda_1 =1\) und somit ist die Wurzelbedingung von Dahlquist in Satz 1.4 verletzt. Dies bedeutet, dass wir unabhängig von der Wahl der \(\beta_i \in \R, i=0,1,2\) des linearen Mehrschrittverfahrens keine Stabilität erwarten können.

3. Alle aus der numerischen Integration gewonnenen linearen Mehrschrittverfahren haben für \(s\in \N^+\) und \(k,r \in \N\) mit \(0 \leq r \leq s\) die Form

   \[u_\tau(t_{k+s}) - u_\tau(t_{k+s-r}) \ = \ \int_{k+s-r}^{k+s} F(t, u(t)) \, \mathrm{d}t \ \approx \ \tau \sum_{i=0}^{r} \beta_i F_{k+s-r+i}.\]

   Daher ist das charakteristische Polynom der zugeordneten linearen Differenzengleichung gegeben durch

   \[\rho(x) \ = \ x^s - x^{s-r} \ = \ x^{s-r}\cdot (x^r - 1).\]

   Dieses Polynom hat \((s-r)\)-fache Nullstelle \(\lambda=0\) und zusätzlich die \(r\)-ten Einheitswurzeln in \(\C\), die alle die Vielfachheit \(1\) haben. Darum sind alle linearen Mehrschrittverfahren die durch numerische Integration gewonnen werden stabil.

4. Für das lineare Mehrschrittverfahren in Beispiel 1.11 lässt sich das charakteristische Polynom der zugeordneten linearen Differenzengleichung angegeben als

   \[\rho(x) \ = \ x^2 - (1+\alpha)x + \alpha.\]

   Dieses Polynom besitzt die beiden Nullstellen \(\lambda_0=1\) und \(\lambda_1=\alpha\). Nach der Wurzelbedingung von Dahlquist müssen wir also für die Stabilität des linearen Mehrschrittverfahrens fordern, dass gilt

   \[-1 \, \leq \, \alpha \, < \, 1.\]

   Wir haben hierbei den Fall \(\alpha = 1\) herausgenommen, da wir sonst eine doppelte Nullstelle erhalten würden, was zu einer Verletzung der Stabilitätsbedingungen führt.